BVDB
In 1961 publiceerde de Franse schrijver Raymond Queneau een bundel met honderdduizend miljard sonnetten. Het boek kreeg de toepasselijke titel Cent mille milliards de poèmes. De wiskundig aangelegden onder u zullen nu wat bedenkelijk kijken. Honderdduizend miljard? Dat is een één met veertien nullen. Als Queneau twintig gedichten per dag schreef, dan had hij bij het ontstaan van het heelal moeten beginnen om op tijd klaar te zijn met zijn collectie. En tóch kon het. De literair aangelegden onder u weten dat een sonnet veertien regels telt, en wie zowel wiskundig als literair is aangelegd, vermoedt dat die veertien nullen geen toeval zijn.
Queneau verzon een slimme vorm: hij schreef tien sonnetten, die allemaal dezelfde rijmklanken gebruiken. Elk gedicht kreeg een eigen pagina, maar elke dichtregel stond op een losse strook papier. Zo kon de lezer zelf een gedicht samenstellen door de stroken om te vouwen, als in de kartonnen kinderboeken waar je het hoofd van een beer op de buik van een giraffe kunt zetten. Veertien dichtregels met elk tien keuzemogelijkheden levert tien tot de veertiende, oftewel honderdduizend miljard, verschillende
sonnetten op.
Bij het maken van zijn dichtbundel riep Queneau de hulp in van wiskundige François Le Lionnais en zo ontstond Oulipo: Ouvroir de littérature potentielle, waarin (vooral Franstalige) schrijvers en wiskundigen samenkwamen. Ze wilden nieuwe structuren en patronen zoeken die schrijvers naar believen konden gebruiken in hun boeken. Hun experimenten leidden bijvoorbeeld tot La Vie mode d’emploi, waarin Georges Perec zijn lezers meeneemt langs de bewoners van een appartementencomplex waarbij de rondgang langs de kamers een paardensprong is, als in het schaakspel. Ook zeer wiskundig is Qui a tué le Duc de Densmore? van Claude Berge, waarin Sherlock Holmes de moord op de graaf van Densmore oplost dankzij een resultaat uit de netwerktheorie.
Maar het meest Oulipiaanse werk is van Queneau zelf: Exercices de style, waarin hij hetzelfde banale verhaaltje in 99 verschillende stijlen vertelt. Hij gebruikt onder andere een sonnet, flaptekst, bewijs en lipogram waarbij de letter e moet worden vermeden. Als wiskundestudent las ik dit boek in de fijne vertaling van Rudy Kousbroek. En geheel volgens de wetten van de serendipiteit kreeg ik in dezelfde tijd het boek The Pythagorean Proposition, waarin Elisha Loomis 367 (!) verschillende bewijzen verzamelt voor de stelling van Pythagoras. Zowel bij verhalen als bij wiskundige bewijzen zijn er talrijke manieren om hetzelfde op te schrijven en het is een kwestie van smaak welke stijl iemand het best bevalt (al is het bijgevoegde meetkundige bewijs voor de stelling van Pythagoras natuurlijk het allermooiste).
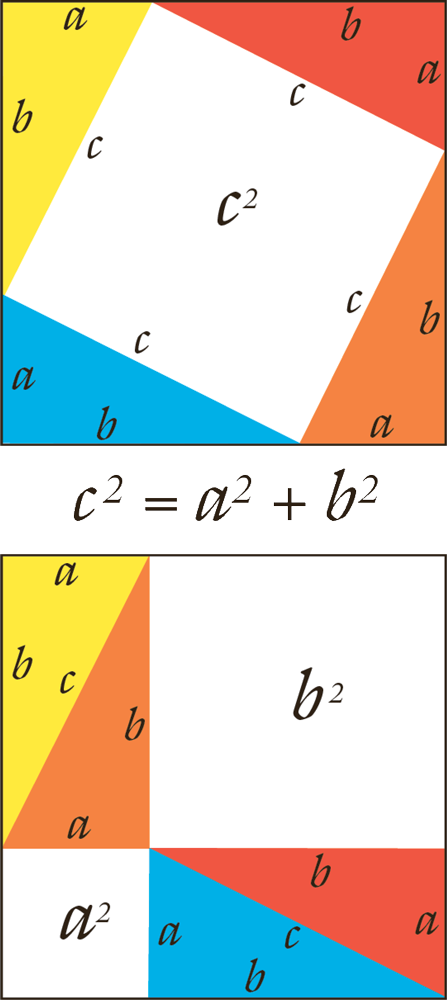
Het mooiste bewijs voor de stelling van Pythagoras
Een ander fijn voorbeeld van serendipiteit was hoe wiskundige Tanya Khovanova en Rutger Kiezebrink van Onze Taal vorig jaar vlak na elkaar twee verwante vragen over rekenen en taal stelden. Kiezebrink verzamelde sommen waarbij het antwoord gelijk is aan het aantal letters van de som. Bijvoorbeeld ‘Zevenhonderdveertig gedeeld door twintig’, dat is zevenendertig gevangen in zevenendertig letters. Of nog mooier: ‘drie maal vier’, want dat zijn twaalf letters, ook nog eens in drie woorden van lengte vier. Of ‘Het kleinste getal dat netjes deelbaar is door twee, drie, vier, vijf en zes’ en zo zou ik nog zeker zestig minuten kunnen doorgaan met voorbeelden. Khovanova had als variant: ‘Uit hoeveel letters bestaat het juiste antwoord op deze vraag?’ Het eenvoudigste antwoord op haar vraag is ‘vier’, want dat heeft vier letters. Maar ook alle sommen van Kiezebrink waren stuk voor stuk een antwoord op de vraag van Khovanova. Dit is de logische voortzetting van Kousbroeks ‘Welke vraag heeft vierendertig letters?’ en het is precies de soort vraag die zowel wiskundigen als taalkundigen verrukt.
Als kind zwijmelde ik boven Opperlands van Battus met al die uitzonderlijke vormen van woorden, keurig geordend per soort. Het is vast geen toeval dat de samensteller óók wiskundige was. Een van mijn favoriete lijsten in het boek was de opsomming van ‘driehonderdendrie prachtige keerwoorden’, met daarin het intrigerende moorddroom. Hoe zou je een soortgelijke vormverzameling met getallen in plaats van woorden moeten maken?Woorden zijn de bouwstenen van onze verhalen, de betekenisvolle combinaties in een eindeloze oceaan van letters. Er zijn bijvoorbeeld 676 mogelijke combinaties van twee letters (26 maal 26), maar het Nederlands telt slechts negentig tweeletterige woorden. De ‘woorden’ van de getallen moeten net zo zeldzaam en betekenisvol zijn. Dat moeten dan de priemgetallen zijn: positieve, gehele getallen die alleen deelbaar zijn door één en zichzelf, zoals 5, 19 of 37. Zij vormen de bouwstenen van alle getallen, elk getal is te schrijven als een unieke vermenigvuldiging van priemen. Daarnaast zijn ze minstens zo zeldzaam en kostbaar als woorden. In de honderd tweecijferige getallen (met de nul aan het begin meegenomen) zitten slechts vijfentwintig priemen.
De tegenhanger van moorddroom moet dus een omkeerbaar priemgetal zijn, zoals 700.666.007. Dat is wel iets korter dan moorddroom met zijn twaalf letters. Sterker nog: er bestaat geen enkel palindroom-priem met exact twaalf cijfers, want een even getal dat omkeerbaar is, is altijd deelbaar door elf (wiskundigen zeggen op zo’n moment graag: het bewijzen hiervan is een huiswerkopgave voor de lezer). Het enige palindroom-priemgetal met een even aantal cijfers is daardoor elf zelf. Priemgetallen hebben nét wat meer regels dan woorden.
Waar bij woorden dit soort speciale eigenschappen afhangen van de taal (een murder dream is geen palindroom, het is niet eens één woord), zo hangt de vorm van een priemgetal af van het gekozen getalstelsel. De voorbeelden hierboven werken alleen omdat wij onze getallen in het tientallig stelsel noteren. Als je 700.666.007 zoals een computer binair schrijft met enen en nullen, dan is het niet omkeerbaar. Al blijft het ondeelbaar, zoals de betekenis van moord in andere talen ook behouden blijft (al zijn er tussen talen dan weer veel meer nuanceverschillen dan tussen getalstelsels).
Tijdens mijn studie ontdekte ik dat wiskundigen ook lange lijsten maken van getallen die zij om de een of andere reden mooi vinden. Zo is 29.137 een bijzonder priemgetal: als je er vanaf links steeds een cijfer afhaalt, krijg je een heel rijtje getallen die stuk voor stuk priem zijn: 9.137, 137, 37 en 7. We noemen een getal met deze eigenschap een links-inkortbare-priem en we weten dat er exact 4.260 van dit soort getallen bestaan. Overigens telt deze tekst precies 1.997 woorden, ook dat is een links-inkortbare-priem. Net als het aantal woorden in deze alinea, telt u dat gerust even na. Je kunt als tegenhanger links-inkortbare-woorden zoeken. Bijvoorbeeld droom dat van room naar oom via om eindigt als m (volgens mij had Opperlands nog geen term voor dit soort woorden).
Dit alles lijkt misschien nogal nutteloos, maar wiskundigen gaan er juist prat op dat hun werk geen praktische toepassingen heeft. Topwiskundige Hendrik Lenstra was eens te gast bij De Wereld Draait Door toen er een nieuw priemgetal was ontdekt. Matthijs van Nieuwkerk stelde de onvermijdelijke vraag ‘wat we daar nu aan hebben’. Lenstra antwoordde vrolijk: ‘Het is gewoon lol. Levensgeluk is ook een toepassing.’ Zo’n zeventig jaar eerder betoogde de Britse wiskundige G.H. Hardy in zijn A Mathematician’s Apology dat de nutteloosheid van fundamentele wiskunde zelfs een pre is: daardoor kan het werk niet misbruikt worden voor oorlog of andere ellende. Bovendien is zuivere wiskunde een intellectuele exercitie, terwijl al het toepasbare in de wiskunde saai en elementair is.
Het is enigszins ironisch dat uitgerekend die priemgetallen, waarvan ook Hardy zeer hield, sinds de opkomst van de computer een overvloed aan toepassingen hebben gevonden. Kennis die eeuwenlang alleen interessant was voor wiskundigen, vormt nu de basis voor allerlei versleutelingen en veilig internetbankieren. Zelfs het tamelijk recente werk van Hendrik Lenstra kent inmiddels allerlei toepassingen, ook al bedacht hij het allemaal puur voor zijn eigen plezier. Zo is het steeds gegaan. Ook al waren in de geschiedenis veel onderzoekers puur geïnteresseerd in de persoonlijke intellectuele bevrediging van hun werk, uiteindelijk hebben al hun nutteloze vragen geleid tot de huidige technologie en welvaart.
Ontdekkingen in de wiskunde zijn een kwestie van begrippen helder definiëren, basisaannames afspreken en daarna volgens de regels ware uitspraken afleiden. Euclides definieerde ruim tweeduizend jaar geleden bijvoorbeeld dingen als ‘de uiteinden van een lijnstuk zijn punten’, nam aan dat door twee punten één rechte lijn gaat en gebruikte regels als ‘als men gelijke dingen optelt bij gelijke dingen, dan zijn de totalen ook gelijk’. Met dit soort eenvoudig gereedschap kon hij bewijzen dat de som van de hoeken in een driehoek altijd 180 graden is of dat er slechts vijf regelmatige veelvlakken bestaan (voor de liefhebbers: dat zijn de tetraëder, kubus, octaëder, dodecaëder en icosaëder).
Regels zijn prachtig en kunnen leiden tot grootse intellectuele prestaties. Helaas hebben ze buiten de wiskunde een wat slecht imago. Regels zouden voor bureaucraten, frikken, kuddedieren of grijze muizen zijn. Terwijl het bedenken van een nieuwe regel juist een zeer creatieve activiteit is. En zelfs het volgen van andermans regels kan zorgen voor een hele reeks nieuwe ideeën, juist omdat het aantal mogelijke denkrichtingen is ingeperkt doordat er een duidelijk kader is waarbinnen je kunt nadenken.
Kortom: maak zelf ook eens honderdduizend miljard sonnetten of schrijf een thriller volgens wiskundige wetten. Zoek getallen die iets bijzonders hebben of verzamel woorden met een speciale eigenschap. Nóg veel beter is het om zelf nieuwe grenzen te bedenken waarbinnen u iets moois kunt creëren. Om te kijken wat er allemaal zou kúnnen bestaan. Zoek net als Oulipo naar regels en patronen en gebruik die vervolgens hoe u maar wilt. Wie weet waar het toe leidt. En vergeet daarbij nooit dat levensgeluk ook een toepassing is.
Ten slotte, ter inspiratie: een eerbetoon aan Rudy Kousbroek die zelf weer een hommage bracht aan Georges Perec. Hierbij 37 versies van dezelfde, banale zin. Sommige varianten volgen beperkingen die de Oulipo bedacht, andere restricties zijn toegevoegd door Kousbroek in De logologische ruimte en vanzelfsprekend zijn er ook regels die ik verzon − u mag zelf raden welke.
Eerbetoon aan Rudy Kousbroek
Oertekst: De kat ligt in de zon.
Meervoud: De katten liggen in de zonnen.
Vermeerdering: De kat ligt in de zonwering.
Anagram (vragend): Zeg, Daniël: ‘Tikt Don?’
Anagram (onthulling): Ad ziet geld in kont.
Anagram (Twitter): Danklied toezingt
Verzamelingenleer: {katten}
{dingen die in de zon liggen} ≠ Ø
Palindroom: De kat ligt in de zon, no, zed nit gil tak Ed.
Ontkenning (1): Er ligt geen kat in de zon.
Ontkenning (2): De kat ligt niet in de zon.
Isovocaal: Ze had jicht, spinde Ron.
Detective: Zijn dat kattenharen op de vensterbank?
Caesarcijfer: Ij pfy qnly ns ij ets.
Lipogram (in A): De poes ligt in de zon.
Lipogram (in E): Kat ligt in zon.
Lipogram (in I): De kat rust onder de zonnestralen.
Lipogram (in O): De kat ligt in het warme licht.
Lipogram (in U): De kat ligt in de zon.
Andere opinie: Ksst, ga eens ergens anders liggen!
A met een aba: Debe kabat ligbigt inbin debe zonbon.
Passief: Er wordt door de kat in de zon gelegen.
Google zoeksuggestie: De kat… uit de boom kijken.
S+7: De katalyse ligt in het zondaarsbankje.
S-7: Het kastpapier ligt in het zomerverblijf.
Alfabetisch (1): De de in kat ligt zon.
Alfabetisch (2): ADDEEGIIKLNNOTTZ.
Andersomliner: De zon. De kat ligt erin.
Plat: Dus ik zeg tegen mijn buurvrouw, buurvrouw zeg ik, weet je dat die kat daar gewoon in de zon leg te leggen?
Isomorf: De kat krabt de krullen van de trap.
Homomorfisme: Denkend aan Holland, zie ik katten in de zon liggen.
Preciezer: De Noorse boskat lag in de namiddagzon.
Germanismen: Mensch, die Katze ligt wie ein lapswans in die Sonne.
Van Dale: Het klein roofdier uit de familie van de katachtigen lag in de stralen van het centrale lichaam in het zonnestelsel waar de aarde deel van uitmaakt.
Dubbelop: De kat en de poes ligt en strekt zich uit in de zon en de stralen.
Fibonacci: O, o, de kat spint achterop vensterbankje.
Oplopend: O, de kat ligt naast zwarte schaduw.
Ivo Niehe: Het is unaniem een belachelijk groot succes hoe de kat in de zon ligt.
Essay
Persoon op plek

Essay
Een smetteloze taal is een onleefbare taal
Essay
Een sterrentaal voor één persoon
Essay
De delicate geest van de uniciteit
Essay
Het einde en een begin
Poëzie
Mitose meiose
Beeld
Gids Galerie: Alon Levin
Grote vragen
Grote vragen
Verhaal
Darling, this place is a lover’s oasis
Verhaal
Iedereen werd verpleegd
Essay
Overtredingen op het dak
Essay
Genees mij!
Poëzie
berichten van de stichting poolvos
Kroniek & Kritiek
